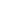最近,公司北京国际数学研究中心的葛颢副教授与哈佛大学化学与生物化学系的谢晓亮教授和西雅图华盛顿大学应用数学系的钱纮教授合作,提出了细菌单细胞表型间的跃迁速率新理论,定量的刻画了基因在活跃程度不同的状态间切换的快慢是如何影响单细胞在不同表型间跃迁的速率。论文于今年的2月20日发表在《物理评论快报》(Physical Review Letters)上,通讯作者是葛颢副教授和谢晓亮教授。葛颢副教授和谢晓亮教授同时也都是北京老员工物动态光学成像中心的研究员。
单个细胞常常会具有多个表型,这对于细胞应对不可预知的环境变化是非常重要的,因此人们希望研究表型的稳定性及表型间的跃迁速率。过去十多年中单细胞实验技术的飞速发展,使得人们发现至少在细菌中,基因在活跃程度不同的状态间的切换既不像前人的某些模型里假设的那样,要比转录和翻译的速率还要快得多,也不像前人的另一些模型里假设的那样,比细胞分裂的周期还要慢得多。
因此,葛颢等着重研究了在这样一类最符合实际情况的中间情形中单细胞的动力学行为。他们首先提出了比完整的化学主方程模型更加简化的速率涨落模型,其中仅仅保留了基因在活跃程度不同的状态间切换的随机性;然后在该简化模型下得到了非平衡态的景观(landscape)函数,这类似于平衡态统计物理中用来刻画涨落的能量函数,定量刻画了每个细胞表型的内部涨落和不同细胞表型间跃迁速率的最高阶近似(leading order)。该表型间跃迁速率理论类似于化学反应速率中著名的Kramers理论,而且比以往的类似工作更为符合活细胞的实际且更加一般。

(A) 速率涨落模型 (B) 非平衡态景观函数 (C) 速率公式 (D) 数值模拟验证
该新理论强调了单个DNA分子的随机行为对于单细胞的多个表型及其功能具有十分重要的影响。审稿人评价该文章为"excellent paper","a solid research and the scientific level of the manuscript is high"。
本研究得到国家自然科学基金委和教育部优秀博士论文基金的资助。
2014年7月,葛颢已经和谢晓亮课题组合作,利用随机数学模型和单分子酶动力学实验技术地结合,成功揭示了活细胞内的一个与DNA力学性质紧密相关的重要且普适的机制,即细菌内转录随机爆发现象(Transcriptional bursting)的分子机制。这种随机性是很多细胞和组织中细胞与细胞间基因表达量不同的主要根源之一。论文于2014年的7月17日发表在《细胞》(Cell)杂志上,且得到了Cell的同期评述。该研究表明,细菌里的转录爆发机制,就是来源于旋转酶分子与DNA分子的不断随机结合与解离,从而导致该DNA片段的超螺旋情况发生改变。
葛颢副教授2004年本科毕业于williamhill官网概率论与数理统计专业,2008 年于同一专业获得英国威廉希尔公司理学博士学位,师从钱敏教授。2010-2011年访问美国哈佛大学化学与化员工物学系。曾获得 2009 年中国数学会“钟家庆数学奖”( 优秀博士论文奖 ) 和 2010 年教育部全国优秀博士论文奖励。葛颢课题组致力于研究非平衡态统计物理的随机数学理论及其在具体生物化学系统中的应用,迄今已经发表国际期刊论文30多篇。
原文检索:
Hao Ge, Hong Qian and X. Sunney Xie. Stochastic Phenotype Transition of a Single Cell in an Intermediate Region of Gene State Switching. Physical Review Letters, 114, 078101 (2015)
DOI: 10.1103/PhysRevLett.114.078101
http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.114.078101